When it comes to learning fractions, some children might take longer to grasp the concept of an amount being less or partially more than a whole number. For this reason, teaching students about fractions might require various different strategies that can reach struggling students. A physical representation of fractions would really help problems come to life in a much more tangible way. It is not easy for a child to understand that sometimes numbers are less than a whole or partially more than a whole. This is the reason we came up with a manipulative that can give a physical representation of parts of a whole. We believe that a physical representation of fractions will help children understand them in a much more tangible way.
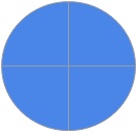
Our manipulative consists of four colored circles; one circle is a whole object with the number 1 on it, the second is split in two with ½ written on it, the third is split in thirds with 1/3 on it, and the fourth is split in four with ¼ on it. The hope of our manipulative is for children to understand parts as being related to wholes as well as wholes being partitioned into parts. Van de Walle et al. (2014) describes, “sometimes the words whole and unit are used interchangeably in discussing fractions, but the unit must be thought about to interpret all the possible concepts that fractions can represent” (p. 204). The user can learn the concept of equipartitioning, where wholes can be partitioned into equal parts. The circles are labeled in order help the child name equal parts upon partitioning.
In order to be successful, children must understand that fractions are not always smaller than a whole. One activity that can be used to help children conceptualize this, while using the manipulative, is what Van de Walle et al. (2014) captions, “More, Less, or Equal to One Whole.” It is stated that students are given a collection of fractional parts (all of the same size pieces). The task is to decide whether the collection is less than one whole, equal to one whole, or greater than one whole. The students will then be asked to draw pictures or use symbols to explain their answer (Activity 12.6, p. 214). Something we have considered is that students who are never exposed to fractions that are greater than one become confused later on when they are confronted with this situation. Van de Walle et al. (2014) mentions that, “The Common Core Standards state that in third grade, students should be able to write whole numbers as fractions and identify fractions that are equivalent to whole numbers.” With that being said, our manipulative can also help students understand situations where there is more than one and challenge them to conceptualize that.
Our project would fail to work if students still believed that fractions are always smaller than a whole, and for example, a fraction such as 4/3 is impossible. While students might easily understand that the full circle that is not broken into pieces represents 1, we also want them to understand it also can represent 3/3. 4/4, or 2/2 and so can all of the other circles when all pieces are put together. If they have trouble seeing the whole circle as if it were all parts of the fraction, then the concept of more than one represented in the manipulative might go over their head. We could consider this a failure and thus need to rework the manipulative to make it easier for children to understand as potentially representing more than just one. A way to combat this would be to provide on a worksheet pictures of circles just like the manipulatives. Those full circles could display 3/3,4/4, and 2/2 as being whole objects but represented in fractions. That way, when we ask students to represent 4/3 or 3/2, with their manipulatives, and then shade in the fraction on the worksheet, they would understand how that happens and be able to explain it.
As stated above, testing for our manipulative could involve partnering the manipulatives with a worksheet to demonstrate their understanding. This would involve students being asked to represent various fractions with their manipulatives and shading in what they made on paper. Another way that they could be tested on this would be to present word problems involving fractions and have them represent the correct answer with the manipulatives. For example, if you ask the students, “My brother, sister, and I wanted pie last night but we wanted to split the pie fairly. Can you show me how much pie we each got?” These types of problems can easily be done with the manipulatives as a tool for students to touch and work with. If students are able to get the correct answer and explain why it makes sense, then we know it was a successful way to work with the manipulative. Another element that students should be able to understand would be to write out the fraction in fraction notation form on the worksheet after shading in the correct amount in the first and second activity. If students are not writing either the correct numerator or denominator, or neither of them correctly they will need more foundational work in fractions.
An obvious limitation to this manipulative is that it only helps children understand ½, ⅓, and ¼ fractions. However, we created this manipulative for children who are just beginning to work with fractions and need that primary framework of smaller fractions that they can easily relate to. Working with halves, thirds, and fourths is something a younger child can definitely understand. Our hope is that younger children can transfer their work with this manipulative onto paper to understand fractions in word problems with ease.
References
Van de Walle, J. A., Karp, K. S., Lovin, L. A. H., & Bay-Williams, J. M. (2014). Teaching Student-centered Mathematics: Developmentally Appropriate Instruction for Grades 3-5 (Vol. 2). Pearson Higher Ed.