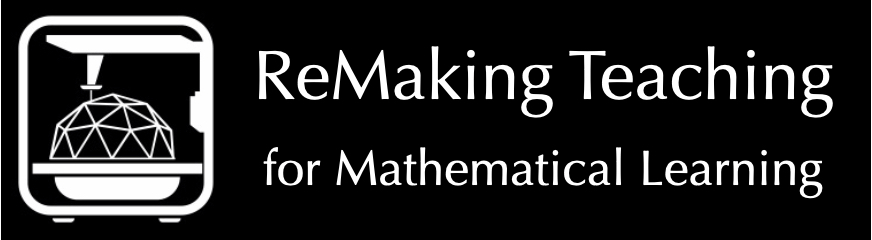Dodecagon Tool
Why/how you think your project should work from a mathematical learning point of view:
We believe our project will work from a mathematical learning point of view. Our design will include children being able to create the complex shape of a dodecagon. Shapes are critical for a child to learn and understand. Shapes are everywhere we look and play a big role in mathematical foundations. Children will be able to break apart and put together the triangles created to form a dodecagon shape.
How is the user of your manipulative supposed to learn from working with your design?
The use of our manipulative will learn from working with our design by learning hands on the different parts of a shape. The student will be able to put together and take apart the model themselves. Instead of viewing geometric shapes on paper or drawing them whole, this manipulative will help students understand the different parts within that shape, and allow them to better visualize the components of each shape they create.
How does the design of your technology reflect your understanding of what mathematics is and of how learning happens?
We want to focus on “the how” one gets an answer. As we stated, this is a hands on learning manipulative. Students can use our model to practice building geometric shapes. The different triangles within in our dodecagon can help students understanding about angles and degrees within geometric shapes and allow them to better understand shapes through their manipulation of them.
What would it mean for your project to be successful in terms of learning?
In order for our project to be successful, the students should be able to understand the concept of geometric shapes. Students should be able to put the dodecagon together and recognize that a 12 sides with angles of 150 degrees represent a dodecagon. Rather than students looking at geometric shapes in a textbook, this allows them to see the shapes in person and gain a more learning experience.
What would it mean if it were to fail to work?
If the pieces of our dodecagon does not fit together or the child doesn’t understand the concept of this project, our design will be unsuccessful. The triangles should fit together form the dodecagon shape. Just by putting the manipulative together, children are learning. With that said, it is unlikely it will fail.
What kind of testing could you imagine carrying out for your design?
Testing for this project will consist of breaking apart and successfully putting back together each piece of our dodecagon. The pieces will be identical triangles that will fit together to form the dodecagon. Connecting these pieces together and having them stick together would be the test. As well as seeing how many different shapes a student could create using the triangles.