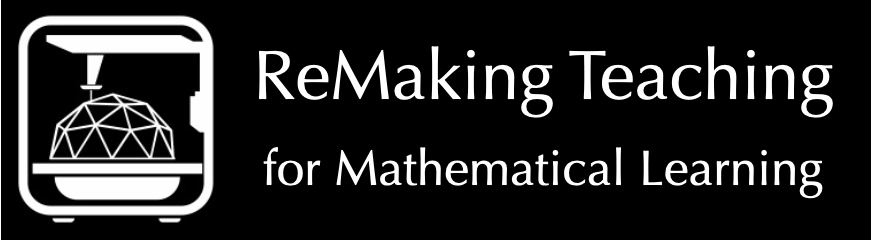Projects – ReMaking Teaching

Math Dragon

September 11, 2020

Click here to download the stl file for this tool. [TBP]

The design of my manipulative is based on the concept of multiplication and the “times table” representation. I have decided to work with these topics primarily because the focus student for my project is beginning to work with multiplication in her second grade classroom. She expressed in my interview with her that she finds the concept of multiplication difficult. Thus, the tool I designed, the Math Dragon, can not only bolster her introduction to mathematics, but also give my student an edge in learning her multiplication facts. My tool’s design is rooted in the Greek myth of the Hydra, a creature which, according to most legends, grew two heads back for every one head cut off. I discovered a relation to multiplication in this design, which my professor later also identified as a model of exponential growth. I could use the dragon to task my focus student with a problem like the following: “If the Math Dragon grows back two heads for every one head cut off, how many heads would it grow back altogether if four heads are cut off?”

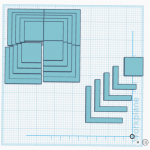
Fraction Rings

September 11, 2020

Click here to download the stl file for this tool. [TBP]

My math manipulative is a variety of rings which each represent different fractions (from 1/2 to 1/8) that are scaled in relation to the pedestal that they go on top of. The relation between fractions with different denominators can be confusing. This manipulative helps students realize that several fractions with different denominators can be composed to make up the whole. This manipulative helps students make sense of fractions with different denominators and the relations between them.

Geometric TouchPoints

September 11, 2020

Click here to download the stl file for this tool. [TBP]

Our manipulative began as an idea stemming from what we learned about our students’ mathematics, which we learned about in our interview with them. We wanted them to learn more about numbers, so we thought it would be a great idea to apply touchpoints to geometric figures. The geometric figures we designed are a square, oval, circle, rhombus, diamond, trapezoid, pentagon, hexagon, an isosceles triangle, equilateral triangle, and a house. We wanted to use them to give students a reason to count. We would ask them to count the sides and the vertices, and maybe see if they could find a relationship between the two numbers.

3D Vertical Fraction Strips

September 11, 2020

Click here to download the stl file for this tool. [TBP]

The manipulative I made is a 3D version of fraction strips. Each strip is a rectangular/square piece that slides onto individual pegs, making them both sturdy and easy to play with. I’ve also made it so that the fraction blocks stack vertically (rather than lining up horizontally), to indicate height as value and amount. I wanted to build something to help the student to visualize and deepen their understanding as they explored fraction relationships. What was most important to me was having all the fractions mounted on one platform with the 1 (whole) always being visible, so that the student could begin to grasp how all the smaller parts relate to the whole.

Place Value Cones

September 11, 2020

Click here to download the stl file for this tool. [TBP]

For my manipulative I have taken something that I have seen being used within classrooms. Many people call them place value cups. Mine are place value cones. The reason I changed it into cones was because my student enjoys art, so I wanted them to look like crayons. I felt that this would interest my student a lot. Besides the look of it, I feel that my manipulative can serve multiple topics and have different purposes. My one hope is that it helps my student learn place value concepts so that they can perform addition and subtraction more meaningfully.

The Area Blocks

September 11, 2020

Click here to download the stl file for this tool. [TBP]

“Research suggests that it is a significant leap for students to move from counting squares inside of a rectangle to the conceptual development of a formula.” I created a tool named “The Area Blocks.” These manipulatives are quadrilaterals with different measures. I believe this manipulative will support the students’ learning because the children will see, touch, and count to find the area of a quadrilateral. They can also compare and contrast areas that have the same numbers of unit squares but have a different measure.

3D Multiplication Table

September 11, 2020

Click here to download the stl file for this tool. [TBP]

The manipulative is a three dimensional multiplication table embedded with tubes so that poles can be inserted at either end, or both ends simultaneously. In using the manipulative, students are provided with a visual representation of multiplicative relationships. The purpose of our manipulative is to support understanding of the mathematics of multiplication and division problems. They will be able to relate the multiples of numbers for multiplication and the factors for division, discover a concept of repeated addition and subtraction, and discover other patterns of their own.

Number Line and Slider

September 11, 2020

Click here to download the stl file for this tool. [TBP]

My manipulative is a number line including the numbers 1-10. It has a sliding piece that goes on top of it that students can use when adding, subtracting, or even finding the number before or after a given number. When the slider is moved over the number line, it highlights just one number by placing the number in the center of the sliding box.

Decimal Snake

September 11, 2020

Click here to download the stl file for this tool. [TBP]

I learned from an interview with a 5th grader that he was struggling with ordering decimals. Ordering decimals requires an understanding of place value. I started thinking about a tool that can help him build a conceptual understanding of how decimal numbers are constructed. During our informal interview, I realized that he likes snakes. So, I decided to create a tool that is interesting to him and will attract his attention and have a mathematical meaning to it. So, I decided to design a decimal snake. The decimal snake consists of 10 pieces. In each piece there will be 10 small increments representing a unit. Having 100 units on the snake will help us to represent decimals in tenths and hundredths place. I created the decimal snake in the hopes that it helps him visualize the meaning of each decimal.

Y Arithmetic

September 11, 2020

Click here to download the stl file for this tool. [TBP]

I designed this tool because my four-year-old student loves shapes, and shapes and patterns are both important and appropriate topics for preschoolers. My manipulatives consist of three large, three-dimensional shapes (triangle, square, and hexagon) each with a “hole” placed throughout the middle of the entire manipulative. In addition, I have 6 thinner manipulatives (3 triangles, 3 squares, and 3 hexagons) each of a different size, yet only one of each shape will fit perfectly through the middle of the larger manipulative of the same shape. I want my student to explore the polyhedra and see the patterns he comes up with.

Shapes for Exploration

September 11, 2020

Click here to download the stl file for this tool. [TBP]

I am designing this tool because my four-year-old student loves shapes, and shapes and patterns are both important and appropriate topics for preschoolers. My manipulatives consist of three large, three-dimensional shapes (triangle, square, and hexagon) each with a “hole” placed throughout the middle of the entire manipulative. In addition, I have 6 thinner manipulatives (3 triangles, 3 squares, and 3 hexagons) each of a different size, yet only one of each shape will fit perfectly through the middle of the larger manipulative of the same shape. I want my student to explore the polyhedra and see the patterns he comes up with.

Rectangular Prism Puzzle

July 23, 2019

Click here to download the stl file for the above picture.

The Maker of the “Rectangular Prism Puzzle” was inspired by a debate among her students over whether or not the parts of a whole could be represented in different ways. She created a manipulative that would “demonstrate [that] portions of a whole can be more complex than a piece of a pizza pie or a plot of land [and would simultaneously] introduce 3-dimensional ‘whole’ pieces to expand their understanding of what fractions can look like.” In addition, the Maker wanted to incorporate the excitement of solving a puzzle into the student’s interaction with the tool. The rectangular prism is made up of 9 pieces, all with equal volume, of which there are seven variations. The Maker suggests using it as an exploratory object for students, allowing them to arrive at their own understandings of the relationship between parts of a whole while experiencing the joy of puzzle-solving.

Ball of Whacks

July 23, 2019

The “Ball of Whacks” is a rhombic triacontahedron with magnetic parts that disassemble into individual rhombic pyramids. It is unique among the Maker projects listed on this website because it is a pre-existing, pre-made object that was purchased for the purpose of the class. The Makers of this project originally wanted to create an object to introduce students to geometry, and help them conceptualize the idea that parts deconstructed from a whole can be put back together in a variety of different ways. Through their design process and inquiry, they discovered the “Ball of Whacks”, and decided to repurpose it as a mathematical manipulative through thoughtful problem solving tasks among different grade levels. The tool also invites students to use it in a creative, playful way. The Makers propose that, in the classroom, “teachers will not tell the children what to create, but rather let them explore the shapes on their own and create their own unique shapes.” Ultimately, the Makers used it as a tool to introduce students to angles, shape variation, and fractions through composition and decomposition.

Grouping Discs

July 23, 2019

Click here to download the stl file for the above picture.

The Maker of the “Grouping Discs” designed a manipulative intended to help students count, add, subtract, and make groups of ten. She explains, “The grouping discs I have created and designed have nine slots in them so that up to nine additional discs can be added to the base disc to make one group of ten. More discs can be inserted into the slots on any of the other discs that are attached to the base disc. By doing so, students can not only add and subtract using direct modeling, they can gain a sense of base ten while also having fun creating their model.” “Grouping Discs” can be a very exciting and expansive manipulative for students as they build grouping and base-ten understandings through dynamic and exploratory interactions with the object.

MultiPartitions Tool

July 23, 2019

Click here to download the stl file for the above picture.

The Maker of the “MultiPartitions Tool” wanted to create a tool that would help engage students in the mathematical ideas of skip counting, multiples and multiplication, fractions, and geometry. She ultimately created a set of tools, and explains, “The manipulatives are comprised of various shapes, and then the shapes are cut into different numbers of pieces based on the number they represent, and each shape has multiple ‘nesting’ layers.” These nested layers will assist the user in skip counting by that particular number as they are added to or taken away from the manipulative. For example, the user explains the case of the number two: “It will show them the starting number of two in the center and then two more outside of that to show four, and then two more to show six, and so on until ten. These shapes will help students visualize how numbers increase when added to themselves.” By understanding multiples, the student will be prepared to gain a deeper understanding of multiplication and division. In addition, the nesting quality of the tool may help students conceptualize fractions. For instance, each layer could be seen as one whole decomposed into 4 fourths. Then the accumulated pieces from 5 layers would represent 5 sets of 4 fourths. The “MultiPartitions Tool”, as evident from its title, refers to both multiples and multiple partitions. It provides a venue for exploring geometric shapes as well, and ultimately serves as a versatile, exciting tool to help students explore mathematical ideas.

Multiplication Decoder Ring

July 23, 2019

Click here to download the stl file for the above picture.

The Maker of the “Multiplication Decoder Ring” describes her tool as a way to help children learn how to multiply in a fun way using both visual and tactile experience. The Maker explains that, “The idea of turning the wheel and visually seeing the numbers in the times table provides a new visual recall to the student. Instead of visualizing a chart, they can recall a moving object with each click of the wheel producing a new number … [It also] allows the student to explore different methods of learning their multiplication tables.” This concrete, physical experience will reinforce concepts through physical integration of learning multiplication facts. The kinesthetic experience of the tool is very important, as the Maker explains when she says, “Moving the wheel the number of times the student wishes to multiply by keeps them engaged in the thought process and allows them to stay mentally and physically engaged in the learning process…the ability to stack the rings allows the student to compare different times tables to learn the differences and similarities of patterns in times tables.” The “Multiplication Decoder Ring” acts as a powerful tool in helping a student solidify their multiplication fact recall abilities.

No Mas Caídas

July 23, 2019

Click here to download the stl file for the above picture

The Makers of the tool “No Mas Caídas” created a manipulative that allows a student to visualize and keep track of their counting. The tool itself has an eye-catching, highly interactive design, and offers the user a dynamic experience as they use marbles to aid in their counting. The Makers say, “The design behind our tool technology [allows] the child to stack whatever piece or object it is that they are working with on top of the other one.” This is important to highlight because the audience can see how this tool would allow students to physically see their work as they add the marbles or any other object into the structure. The elegance and utility of the tool is explained through example by the Makers: “Without having to count all twenty-one objects in total, the student could use the ruler to see almost instantly what twelve blocks looks like against the ruler… It also helps students make sense of number decomposition, as the ruler can help students recognize how the counting numbers are embedded in each other, allowing the student to construct knowledge that will be useful in breaking numbers apart (and together).” “No Mas Caídas” is an exciting, culturally relevant, and interactive tool that engages children and allows them to construct their own strategies and understandings of quantities, addition, and subtraction.

Fraction Orange

July 23, 2019

Click here to download the stl file for the above picture.

The Maker of the “Fraction Orange” created a manipulative with the intention of building a “physical understanding and conceptualization of fractions” in the user. She explains that it “is intended to help children understand how parts can interact with their whole in order to help them conceptualize dealing with fractions on a deeper level.” Through interactions with the tool, a student will be able to explore the physical experience of their own fraction strategies and ideas, and aid them in comparing fractions and fraction division problems. The tool is also meant to be used in an exploratory way, and in doing so, the user will be able to make sense of the nested nature of the pieces in order to experience how its pieces are partitions of a whole. The Maker explains, “As the child starts to uncover (dare I say “peel”) the different compartments of the orange, they will discover how a whole can be divided into different parts (slices) equally.” In contrast to flat, linear traditional fraction strips, the “Fraction Orange” gives children the opportunity to experience concrete, kinesthetic representations of concepts, which will in turn build their understandings of the relational qualities of fractions.

Connect 10

July 23, 2019

Click here to download the stl file for the above picture.

The Maker of “Connect 10” tells us that she created a manipulative in order to help students gain “a better understanding visually of multiplication, [which in turn will] allow the user to gain a better understanding of multiplication facts.” By using “Connect 10”, the user will be given the opportunity to explore the concepts of multiplication in a way that will provide them with flexible thinking rather than reliance on the typical memorization of multiplication tables. The Maker explains its use: “The user will use the manipulative to build their way from a factor to a product by finding the missing factor. They will be able to visually see the starting factor and how they will be able to get to the end or product. The array that they will have to create will allow for them to know what this missing factor is. This will be done by having to create a [rectangular] figure.” It is important to point out that the maker of this tool wanted to create something familiar that would invite students to interact with it while they work towards finding solutions and building mathematical connections.

3D Hundreds Chart

July 23, 2019

Click here to download the stl file for the above picture.

The Makers of the “3D Hundreds Chart” designed a tool to help students visualize and experience their learning of base-10 concepts and rounding numbers to the nearest tens place. The Makers explain, “If a child is asked to estimate the number 6 to the nearest tenth, they can use [the] manipulative to fill 6 small individually carved out spaces to be able to see there are only 4 spaces more to get to 10 and 6 spaces to go back to zero… By inserting manipulatives into the individually carved out spaces on the chart, [students are] able to see where a particular number falls to understand if the number should be rounded up or down to the nearest tenth.” This type of problem is facilitated by interaction with the manipulative, as it was created to assist the students through productive struggle in order to develop their own strategies to find solutions. Another important aspect of tool is that the “‘3D Hundreds Chart’ allows the user to understand numbers in a variety of ways including understanding numbers as individual units of ones and also understanding numbers as groups of tens.” This is a vital concept for students to learn in order to understand place value and other subsequent mathematical ideas.

Samantha Circles

July 23, 2019

Click here to download the stl file for the above picture.

The Maker of “Samantha Circles,” designed a tool intended to facilitate student understanding of fractions. She explains the structure of the object: “My design is a series of rings that rest on a cylinder. The rings are the main aspect of the design, the cylinder is merely for storage and to assist in manipulation.” The tool allows the user to move the rings in relation to one another in order to compare different fractions between 0 and 1. The Maker that her motivation behind the design was that “for many students, they understand numbers, but fractions are tricky because they require students to visualize that bigger numbers are actually smaller, and smaller numbers are bigger.” “Samantha Circles” provides the user with a tangible experience of this concept. In addition, the Maker explains, “Each student could use it in a completely different way to achieve the same result, and that was my main goal with this manipulative.” This illustrates that the tool has its own magic, and that a student can use it in a variety of ways to arrive at their own solution. Finally, the tool’s unique shape is intriguing and promotes student interest in the manipulative, prompting them to explore in order to gain deeper mathematical understandings.

Dodecagon Tool

February 16, 2017

Why/how you think your project should work from a mathematical learning point of view:

We believe our project will work from a mathematical learning point of view. Our design will include children being able to create the complex shape of a dodecagon. Shapes are critical for a child to learn and understand. Shapes are everywhere we look and play a big role in mathematical foundations. Children will be able to break apart and put together the triangles created to form a dodecagon shape.

How is the user of your manipulative supposed to learn from working with your design?

The use of our manipulative will learn from working with our design by learning hands on the different parts of a shape. The student will be able to put together and take apart the model themselves. Instead of viewing geometric shapes on paper or drawing them whole, this manipulative will help students understand the different parts within that shape, and allow them to better visualize the components of each shape they create.

How does the design of your technology reflect your understanding of what mathematics is and of how learning happens?

We want to focus on “the how” one gets an answer. As we stated, this is a hands on learning manipulative. Students can use our model to practice building geometric shapes. The different triangles within in our dodecagon can help students understanding about angles and degrees within geometric shapes and allow them to better understand shapes through their manipulation of them.

What would it mean for your project to be successful in terms of learning?

In order for our project to be successful, the students should be able to understand the concept of geometric shapes. Students should be able to put the dodecagon together and recognize that a 12 sides with angles of 150 degrees represent a dodecagon. Rather than students looking at geometric shapes in a textbook, this allows them to see the shapes in person and gain a more learning experience.

What would it mean if it were to fail to work?

If the pieces of our dodecagon does not fit together or the child doesn’t understand the concept of this project, our design will be unsuccessful. The triangles should fit together form the dodecagon shape. Just by putting the manipulative together, children are learning. With that said, it is unlikely it will fail.

What kind of testing could you imagine carrying out for your design?

Testing for this project will consist of breaking apart and successfully putting back together each piece of our dodecagon. The pieces will be identical triangles that will fit together to form the dodecagon. Connecting these pieces together and having them stick together would be the test. As well as seeing how many different shapes a student could create using the triangles.

Base Ten Tool

February 16, 2017

As I was thinking about what to do for this project, I looked back at the lessons that interested me. The lesson that stood out to me most was that of base-ten concepts. Growing up, I’d grown accustomed to using base-ten concepts to solve problems in addition, subtraction, multiplication, and division. When we were using the base-ten blocks to visualize how a young child would learn base ten concepts, it became clear to me that would be the direction my project would lean towards. I loved the idea of grouping based on each place (ones, tens, hundreds, etc.). In order to clearly demonstrate base-ten concepts, with unifix blocks, one can’t use more than 9 of each unit block. If there was a group of more than 13 ten sticks for example, it would have to be replaced by grouping 10 tens, getting rid of them, and replacing them with a 1 hundred square. The end result would be a 1 hundred square and 3 tens sticks to make 130. Hence, I came up with a base-ten calculator of four prongs for the base-ten places from one to a thousand, which for the rules of this model would only allow for 9 rings to fit in each prong. However, there will be 18 rings for each place value and each group of 18 rings has a color that corresponds to its place value.

The idea of this design is that the user would demonstrate their knowledge of base-ten concepts by grouping when adding, subtracting, and multiplying. The first thing the user would have to do for a problem like 123 + 98 is to place 1 hundred ring in the hundreds prong, two tens rings in the tens prong, and place 3 ones rings in the ones prong. After that the user can do two things. She can add 98 by adding 8 ones rings to the ones prong, taking a group of 10 out and replacing it with a tens ring in the tens prong, adding 9 tens rings to the tens prong, and taking out a group of 10 and replacing it with 1 hundred ring in the hundreds prong. She can also add 9 tens rings to the tens prong first, take out a group of 10 and replacing it with a 1 hundred ring in the hundreds prong, add the 8 ones rings to the ones prong second, and then take out a group of 10 and replacing it with 1 tens ring in the tens prong. There would be 2 rings in the hundreds prong, 2 rings in the tens prong, and 1 ring in the ones prong.

When the user multiplies, she would ideally be adding the multiplicand x amount of times. When subtracting, the user might have to create more groups of 10 for a place value if that place value is being subtracted by a larger number. This is an active learning experience to see why addition, subtraction, and multiplication works in the way schools teach them. This design shows that base-ten concepts require grouping and adding or subtracting those groups of ten to place values depending on the problem. The way students learn how something works is if they do it hands on. This model is a hands on calculator for understand base-ten concepts. They would see for themselves why we borrow when subtracting and adding more tens when adding larger place value numbers.

If the manipulative that is created is successful, then this manipulative worked in aiding students in visualizing and learning the mathematical principles around base ten grouping. One of the most important concepts of base ten to recognize is larger quantities are seen as units made up of smaller units. If successful this calculator allowed students to visually understand how units of tens are grouped together to make larger units such as hundreds, and thousands. The rings used would teach students’ relational understanding of place value through direct modeling representation. If students could demonstrate on this calculator how each ring not only means one, but simultaneously on a different rod mean one, ten, hundred, and thousand then they are demonstrating their learning around multiple ways to utilize grouping. Not only understanding place value as a written or spoken concept, but also understanding that number symbols have various values depending where it’s placed numerically in a number sequence will be correctly demonstrated utilizing this tool. The students’ flexibility in thinking in multi digit numbers when it comes to grouping would be successfully supported in this test design that’s engineered to allow students to see the way grouping occurs in more complex numbers. If there is learning with this tool as observers we should see students independently utilize the tool to figure out an arrayment of problems of different complexities.

If the tool fails to work then we know as engineers the individual placeholders rings didn’t support relational thinking as we thought. The transferring of the rings from one rod to the next when solving problems could have been befuddling. We know the meaning of the rings as being associated with a unit that represents a measurable unit that is larger than the one single placeholder object was not understood. Unlike blocks that show direct modeling of individual ones, rows of tens, or hundred grids this calculator has the same individual ring that represents multiple units values. Base ten blocks that are singular like our rings still are stacked in rows of individual ones that make up rows of ten for the child to visually remember and be able to count out by ones the number as a whole. Our rings rely on the student understanding that each ring value is contingent on what labeled rod it is on. Another possible malfunction is the calculator can make the students confused if they lose their counting when transferring rings during addition, subtraction, and multiplication problems. With every new tool there are kinks to be fixed by testing the product and taking it from theory to actual implementation.

With each child having a complex mind with multiple ways of thinking, the way we plan to test our manipulative can show us how the tool is being used, where it aids in learning, and how it can be fixed in places it falls short of being productive. We plan to create a group of testing problems that analyzes how well our tool helps students with simple one digit problems, then two digit, three digit, and finally four digit modeling. We can do an arrangement of addition, subtraction, multiplication, and division to also see what types of problems the tool is best constructed for. After seeing the initial use of it with just written representation problems, we will test the tool against all the word problem choices we learned from our cognitively guided instruction problem types such as join result unknown, joint change unknown, separate result unknown, separate change unknown, part-part whole, whole part unknown, part part whole, part unknown, compare referent unknown, and compare difference unknown. Understanding strategies for these problems and learning how to understand our student’s thinking from leading them to reflect on their own strategies, we can see how the tool is used and if it might not be helpful for certain problems. During this testing we would take anecdotal notes on the child’s interaction with the tool as well as their thought process with working with the manipulative.

This tool would prove to be advantageous to older students who benefit from using modeling, but are often geared towards written representation strategies that make them more accustomed to regurgitating algorithm methods. As students advance in their learning they are often forced to give up strategies that helped them effectively answer mathematical equations beforehand, and are pushed to approach new problems with one method. This invention would give a more complex direct modeling tool that could be used during tackling advanced math problems. With multiple ways of thinking and learning, education doesn’t have to become uniform to one way of learning or solving problems, but can be opened to using newer technology that supports kinetic learners at any age. With the push to differentiating teaching and UDL classrooms, this tool can be used to create inclusivity in the classroom and support all learners that derive at answers differently.

“The Elevator”

February 16, 2017

My project will be a number line that consists of positive and negative numbers. The number line will be vertical instead of horizontal to act as an elevator chute. There will be another piece that can slide up or down according to the problem that the student is working on. This extra piece of the manipulative will be considered the “elevator.” The idea of this number line is to help students physically picture how to add and subtract positive and negative numbers. It is easier for students to understand concepts in math when they can relate to the content. This is why I chose to use an elevator, because I can assume that most of the students have at some point come in contact with an elevator in their lives. On the elevator there will be symbols of up and down arrows and a positive and negative sign so that the students can determine which way the elevator should go according to the problem. The 0 on the number line represents the ground level. All the positive numbers represent different floors above the ground level, and all the negative numbers represent different floors below ground level, or in the basement.

When the student uses this manipulative, they can physically move the “elevator” up and down the floors. For an addition problem such as, -5+2, the student will start the “elevator” at the mark where it says -5. This indicates that it is 5 levels under ground level. Since the problem asks the student to add 2, the elevator will move up 2 “floors” and the student will see that the answer is -3.

As a student I struggled with learning how to add and subtract negative numbers. It was a concept that I always needed to draw a number line and count on the number line to solve. What confused me the most was when adding to a negative number it was hard for me to conceive that the actual number would be a smaller digit. For example -6 + 3, I would always solve it to be -9 because adding meant bigger numbers so, -3 as the answer didn’t make sense to me. My background in learning how to add and subtract negative numbers is why I came up with this idea. Having the number line be a vertical manipulative and reference an elevator explains why when you are adding to a negative number, you need to go up towards the ground level. This will result in a “smaller” digit but of course the value of this digit is bigger, because it is “higher ground”.

Children use direct modeling to solve problems that may be more difficult to them. They are able to take the problem step by step and get to the answer. This manipulative will do exactly that. Each problem, the student will start on the number line with the first digit given, and depending on what is being asked they will move the “elevator” in that direction. If this project were to fail I would try using a different concept for the number line. Instead of using an elevator chute, I could make reference to something else they may be learning in a different subject. For example, if they are learning about the different layers of Earth and the atmosphere in Science class, I could make each level pertain to each of those layers.

Some testing that I would carry out for this manipulative is to give them worksheets of problems that they would be able to use this number line. After enough practice, I could quiz them on adding and subtracting negative numbers without the manipulative to see if the idea of negative numbers sticks. Fortunately, it is very easy for a student to draw this manipulative on a piece of paper in the event that they do not have the actual manipulative to use. If they become stuck on a problem, they simply have to create a vertical number line and count the correct amount of “floors” up or down. The hope is they will not have to physically see the number line, but can reference an elevator in their minds, and associate the numbers with different floors in a building to come up with the right answer.

Time Tool

February 16, 2017

The manipulative that I will be creating will be a tool for students to think, learn and solve problems about time. I will be using the same concept of fraction circles, yet instead of labeling them with a fraction, they will be labeled with minutes. For instance, a whole circle will be labeled “1 hour”, while two half circles will be labeled “30 minutes”. I will also have circles fractions for 15 and 5 minutes. Though I thought about doing 1 minute pieces, I would fear that they would be too small and for the purposes of teaching young children, may also not be safe.

The main goal of this projects is to give a concrete representation of the relationship between hours and minutes. Using manipulatives is especially important when exploring new concepts, and sense time is a very abstract concept, it is especially pertinent that students have something concrete to work with (Van de Walle et al., 2014). With these manipulatives, students will be better able to solve addition, subtraction, multiplication and division problems relating to time. For instance a child may be confronted with a problem such as this:

Bob has four homework assignments. It will take him 45 minutes to finish each assignment. How many hours of homework does Bob have in total?

As stated in Teaching Student-Centered Mathematics, a study by Blume, Galindo and Walcott found that on the 2003 NAEP assessment, “only 26 percent of fourth graders and 55 percent of eighth-grade students could solve a problem involving the conversion of one measurement of time to another” (2014). With Minute Minis, students would theoretically be able to make this conversion by using the pieces to model and solve the problem. A potential way this could be modeled would be using one 30 minute piece and a 15 minute piece to show 45 minutes, then replicating this 3 other times to show 4×45. A child might then notice that they can make 2 wholes – hours in this case – using 4 of the 30 minute pieces and 1 whole/hour using the four 15 minute pieces, leading them to an answer of 3 hours.

Another potential use for Minute Minis is to use them to introduce clock reading. According to the Common Core, students are only exposed to clocks to the hour or half hour in 1st grade and then later exposed to the nearest 5 minutes in 2nd (2016). As Van de Walle et al. explains, a student who can identify 2:30 may initially be challenged by 2:33 (2014). Likely, this is because students don’t know what 2:30 means; they might not be able to make the connection that 2:30 is 30 minutes past 2:00 or have any concept of how minutes relate to hours. The reason why I decided to design my manipulatives in likeness of fraction circles was to ensure that they could easily translate to the face of a clock. It is my hope that students would be able to use the Minute Minis directly on the face of a clock provided by the teacher to explore the relationship between where the minute hand is pointing and the number of minutes past the hour. In other words, students can use the pieces to help them count, i.e. “I know that when the minute hand is pointing at the 4, it is 20 minutes past the hour because 15+5=20. I started at the 12 on the clock and put a 15 minute and a 5 minute piece to get to 4.” I also wanted to ensure that I used fractions that would equate to important benchmark times (15 minutes, 30 minutes), something that Van de Walle states is important in becoming a proficient clock reader (2014).

Overall, Mini Minutes would allow students to work with time in a concrete fashion using their own uniques strategies. If Mini Minutes is a success, students would be able to begin reading time and solve problems involving time, though not without proper support. Students need to have a thorough understanding of the concept of time to be able to effectively work with manipulatives (Van de Walle et al., 2014). For example, if a student were to use these manipulatives to read the time on a clock, they would first have to understand the different parts of a clock, what direction the clock spins in, etc. If they did not, using the manipulatives would likely fail to help the child understand and solve problems with time.

As for how I intend on testing this, I happen to be giving a lesson on reading clocks in my placement in a few weeks and – if my cooperative teacher allows it – I would love to somehow incorporate my manipulatives in the classroom as a way to gage what my students know about time. Currently, most of the 2nd graders in my class can tell time to the nearest half hour, yet I am unsure of how they know how to do this. Is it just because they know that when the minute hand is pointing at the 6 I say _:30 and when it’s pointing at the 12 I say _:00? Or do they have a more deeper understanding of time and how a clock works? For example, a child in my placement who did not know the direction an analog clock goes, might use the pieces to count the minutes by starting at the 12, but going the opposite direction. This may lead them to believe that when the minute hand is pointing at the 9, that is 15 minutes past the hour. However, a child who has a deeper understanding, may be able to use the manipulatives to tell time to the nearest 5 minutes, even when they have only been taught to read time to the nearest half hour. This will help me craft a lesson plan that will build on what they know.

Work Cited

Standards for Mathematical Practice. Common Core State Standards Initiative. (2016).

Retrieved October 27, 2016, from http://www.corestandards.org/Math/Practice/

Teaching Student-Centered Mathematics: Developmentally Appropriate Instruction for

Grades 3–5, 2nd Edition. Van de Walle, J., Karp, K., LouAnn, L., & Bay-Williams, J.

(2014). Boston, MA: Pearson. [ISBN-13: 978-0132824876]

“The Hexahedron Cube”

February 16, 2017

The manipulative we are going to make is a 10x10x10 cube that will help students learn multiplication by counting the cubes. A cube has length, width, and height, and with our cube manipulative children will be able to learn how to multiply two numbers by length x width by counting the number of cubes in the rows and columns. This will also introduce them to the area of a cube. This will also apply to three numbers that will include length x width x height that will teach them the volume of a cube. In all the children, will learn the multiplication of 2 and 3 numbers together. As the children count the blocks, they will be learning as well as gearing their interest into the cube and wanting to become engaged in how to multiply.

How the user of your manipulative is supposed to learn from working with your design?

The purpose of the cube is to teach children how to multiply 2 and 3 numbers using this cube. The 10x10x10 cube is designed such that the entire cube will have sub cubes of 1x1x1. The child will then count the number of small blocks/cubes to multiply.

How does the design of your technology reflect your understanding of what mathematics is and of how learning happens?

Our design reflects learning using direct interaction in the environment and using our cube. We have created an abstract structure that has attributes and properties that will help children learn to multiply, and helps them in the cognitive process of learning. Our technology design will keep children engaged, while also increasing their interest and enjoyment in understanding math. Learning happens when children begin to have conceptual understanding. When we allow for the student to work with our cube we want them to develop ideas, and create their own strategies for learning and understanding the concept we present to them. Learning and understanding math also happens when there is confidence. Our main priority for students using the manipulatives is to feel confident that they will be able to multiply, and find this learning fun and resourceful.

What would it mean for your project to be successful in terms of learning?

Our projects success is based on how well the children respond to the manipulative design. In terms of learning the students would need to reflect that they understand what is presented before them, and that our cubes engage them. In an effort for the students to learn our cube needs to have the proper content that will allow the children to be able to learn to multiply. The tool will need to be meaningful to their learning and understanding of how to multiply two and three numbers. This projects success is also based on how the students can make connections from the multiplications to other areas, as well as the strategies they could come up with. If the project is successful, the students will build multiplication skills. They should also build inquiry from it. The students should be able to reflect on what they have gathered from working with the manipulative, how they have learned from it, and how they can use this to help them with everyday multiplication academics. The success of the cube would finally come from how the student explanation of how they learned. If the manipulative was well understood, we will also check for understanding when the tool is not being used.

What would it mean if it were to fail to work?

If the tool failed to work it would mean that maybe the cube was confusing for the student to understand. It could also mean that it did not meet the expectations we were hoping for, and that we did not foresee future setbacks with the cube. It could also mean that the cube was not at the child’s developmental level. Another possible reason it failed to work would be that it could have been time consuming.

What kind of testing could you imagine carrying out for your design?

We are planning to do below two test cases:

Verify multiplication of 10×10 holds. We will pick any one face of the 10x10x10 cube and count the total number of 1x1x1 sub cubes in it. There should be a total of 100 cubes.
Verify multiplication of 3x4x5 holds. We will carve out a 3x4x5 cross section and then further divide it into three 1x4x5 stackable cubes. Upon physical counting, there should be a total of sixty 1x1x1 cubes, which would verify that multiplication holds.

Modified Fraction Circle

February 16, 2017

The learning tool I have created is a modified form of a fraction circle. Typically, fraction circles are designed with entirely equal parts; that is, a fraction circle will represent (for example) thirds or quarters and be broken into three or four equal parts respectively. While this has educational value in its own right, the modified form I have devised is composed of varying fraction sizes within the circle. Specifically, this fraction circle is a representation of the division of duples. The largest piece represents a half, but rather than the other piece also being a half, it is broken into quarters. One of these quarters is broken into eighths, and one of the eighths is broken into sixteenths. Though this tool is restricted to only demonstrating a division of two, it has its own purpose that standard fraction circles are not able to achieve. Not only does it allow the learner to be able to visually compare the different sized fractions composing the whole circle, but it allows for them to also understand the relative proportionality of each piece (two eighths make a quarter, two quarters make a half, etc.). This allows for this one tool to be used in various contexts and for various fractional proportions—likely with greater application than a standard fraction circle. Additionally, since divisions by half are so common in the world around us, there are many potential cross-curricular tie-ins (such as to music and the division of rhythmic beat units in duple meters), and real-world applications (such as to measurement and the division of inches in the Standard system).

With this tool, the learner is not limited to visualizing how all the parts collectively make a whole (as is the case with typical fraction circles). In one possible application, the student can use smaller parts and put them together to create other fractions of the circle. For instance, they can take the two one sixteenth pieces and put them together to not only form one eighth, but also relate them to the existing one eighth piece in order to visualize the comparative size. Providing learners visuals while teaching fractions is essential in helping them understand these concepts. For example, as Van de Walle et al. (2014) points out, “students may be told the bigger the denominator, the smaller the fraction. Teaching such rules…may lead them to overgeneralize that 1/5 is greater than 7/10.” In this way, students are missing essential learning opportunities when they are not provided with visuals and are limited to verbal explanations of rules. This modification of the fraction circle allows for yet another visual and kinetic tool to be used in the classroom encouraging learning, and for expansion to second and third level proportional associations.

Students must be provided with concrete tools to help them grasp these concepts. Van de Wall et al. (2014) also finds that, “students often do not explore fractions with a variety of models or do not have sufficient time to connect the models to related concepts. In fact, what appears to be critical in learning is that the use of physical tools leads to the use of mental models, and this builds students’ understanding of fractions.” This tool supports students in their exploration in understanding mathematical concepts and relationships. The teacher plays a critical role in mediating the use of mathematical learning tools which can enhance students’ learning. As was mentioned previously, once students are able to visualize the relative proportionality of various divisions of two through use of this manipulative, they will then be more likely to be able to successfully solve problems that include fractions, and, to Van de Wall’s point, will be able to apply this knowledge to other disciplines and applications in which these proportions appear.

To this end, successful application of this manipulative would be twofold. Firstly, learners will have an understanding of fractions and the concept of how fractions operate. At the base level, the student would be able to use trial and error to compare equal parts. Additionally, learners are able to build upon prior knowledge of whole numbers to be able to show how fractions are alike and different within whole numbers. As was noted earlier, since the tool will provide two of the same sized part (one sixteenth), they will be able to see that these two parts combined are equal in size to one eighth. These two eighths are then equal to a quarter. Next, these two quarters create a half, mirroring the piece of the manipulative representing one half. Ultimately, we want students to be able to grasp how fractions, when combined, create a whole. We want them to understand how the whole is composed by which pieces, or fractions, that they come to discover on their own and eventually are able to create a mental image of. Additionally, they should gain the perception that fractional pieces themselves are made up of other, smaller fractions—a property this tool demonstrates that existing fraction circles often do not.

Second, and perhaps more importantly, students will be able to use this knowledge in real-world applications. A logical extension activity (once the basic understanding of division and multiplication of fractions by two is understood) would be to the Standard ruler. This manipulative (alone or in multiples if measurements larger than one are involved) could be used to demonstrate and calculate addition and subtraction of fractions of an inch. Often young learners can struggle with this concept at first, and the use of a manipulative designed in this way could prove quite successful towards providing a concrete, visual means of assisting in these types of calculations of measurement that are necessary in virtually every walk of life.

Failure of the design to work would be evident in the original application of the tool. While it would be tempting to use successful completion of an extension activity (such as adding and subtracting measurements) to evaluate the success of this design, too many variables are at play for this to be a conclusive assessment on its own. Rather, the use of the tool itself is the best judge. Students should be able to use this tool to understand the relative proportions of halves, halves of halves, etc. Any duple divisions (up to sixteenths) and how they relate to their counterparts in the fraction circle should be fair for assessment after implementation of this tool. If the majority of students are unable to understand this concept, then the tool would have failed.

As such, testing of the tool should begin by probing students’ understanding of this concept. Through various questions (perhaps related to circular foods, such as pie), starting at the very base level (“what piece represents a quarter of the pie?” and “what piece represents half of that?”), ultimately we would want students to be able to answer questions constructed in the following form:

“If you have half of a pie, and you split your piece in half to give one piece to a friend, what fraction of the whole pie do you still have?”

This tests multi-layered understanding of fractions and their proportions to one another and examines the ability to make second and third tier determinations as to fractions—the essential goal of the tool. Use of the manipulative should culminate in a thorough understanding of this concept, and a successful test is one in which this knowledge is demonstrated.

Once this has been determined to have been achieved, application and implementation of this knowledge via the previously mentioned extension activity involving use of the manipulative as a visual aide in computation of problems concerning the addition and subtraction of measurement could adequately test the secondary goals of its function. Problems could begin by asking what one eighth of an inch plus one eighth of an inch is equal to, and progress to more complex problems that include whole numbers (such as 1 and 1 quarter inches plus 2 and 1 eighth inches). If students are ultimately successful solving these types of equations, then the manipulative would have been proven to work not only at its basest level, but also in its secondary function as a visual aide in application.

Addition and Subtraction Number Line

February 16, 2017

The learning tool we have re-created is a number line that helps children solve addition and subtraction problems up to the number 20 without using paper and pencil. The number line would be blue with black numbers 1-20. Then, we would create two separate points so the student is able to jump forward and back. Green would represent addition and red would represent subtraction. The advantage of using this number line is to show a tool for helping children develop mental arithmetic with smaller numbers. Our grade level would focus on 1st grade. We decided to use two points so that the student wouldn’t get confused. The green point would move from left to right where as the red point would move right to left. We were thinking in terms of how the number line is written out ,we count forward towards 20 for addition and when we subtract we count backwards towards 1.

When beginning to learn adding and subtraction children may use the number line to find the answers before they can do it automatically in their heads. For example, the answer to the subtraction problem 18-5; equals 13. Once a student sees this visually it very well can help with math concepts. They are made aware of the difference between these two numbers by looking on the number line. It can start to make sense for these young learners. Many students need concrete examples of how to solve problems in mathematics. As stated in our book, many students will use counters, bar diagrams, or number lines(models) to solve story problems. The model is a thinking tool that helps them both understand what is happening in the problem and means for keeping track of the numbers and steps in solving the problem. Van de Walle et al. (2014).

Teachers use many forms of technology to teach students. For example, smart boards, tablets and computers. Technology is becoming more prominent in today’s classrooms. In mathematics, these tools can be very useful for teachers in engaging students to new material and lessons. Using technology to get students engaged in a mathematical lessons can be done with the use of our number line, which is a form of technology. We consider this to be a concrete manipulative that reinforces a mathematical concept of number sense.

The number line can be overlooked in many classrooms, applying it with technology can make it more appealing for these young learners. The number line can be a very effective tool for memorizing and practicing counting with numbers. When a student can visually watch the jumps forward or backwards representing adding and subtracting, number operations can make sense. Children appeal to things that are bright and colorful, we hope they will be more inclined to focus on our tool because it’s not monotone or as blain as paper and pencil.

We think one of the indicators that our class is learning is if they are getting an equation, 4 + 3 and knowing they can start from 4 on the number line. They would continue by adding 3 to get an answer of 7. Sometimes children will start on their fingers counting to 4 and then adding 3 more. The number line is a tool to facilitate adding and subtracting. Eventually the children could have a mental image of the number line and be able to automatically add or subtract numbers to 20. Some ways we will implement support is: Avoid revealing whether the student’s answer is right or wrong, let students share their thinking freely without interruption and ask students to demonstrate their understanding in multiple ways. Van de Walle et al. (2014)

One way to assure that our number line is effective and productive we would have to use a rubric that shows the students understanding of this tool is working. “A rubric consists of a scale based on predetermined criteria with two important functions to see what is central to excellent performance, and (2) it provides the teacher with scoring guidelines that support analysis of students’ work.” Van de Walle et al. (2014). For example, the students need to be able to use logical reasoning, expressed a grasp of numerical relationships and structure and solve the problems accurately and effectively.

As opposed to asking what it would mean if the manipulative were to fail. I think a better question could be finding out the cause of why it didn’t work. Experimenting from the beginning steps where it went wrong might be a good place to start. We would have to consider if the design is not simple enough for a first grader to understand the concept of this number line. Were we able to explain it in a way that was not to complex and with minimal simple steps. Is the design over whelming at first sight, which is not what the design is supposed to do. This design should be simple in the since that it has clearly identified parts. The number line is blue with large enough numbers that are identified. The moving parts are simple as well, Green represents addition and Red represents subtraction. The number line is to work the same ways as if done with paper but things are in color so the student can clearly identify what strategy they are conducting when using the number line.

To test the number line, we would start off with simple problems: 6+1=7 or 5+3=8. Explain to the students that when adding we count from left to right on the number line. The green point is what represents addition. So if that counter is not moving left to right, their answer will not be correct. Simple examples of subtraction would be: 5-3=2 or 10-4=6. When subtracting the points move from right to left on the number line. The red point represent subtraction so if the counter does not move from left to right then its not subtraction. For examples of complex addition and subtraction problems to solve:
Problem 1:    8+ __= 20
We have to start at eight and end at 20. How many jumps do we need to get to 20?   We would do the jumps in green. We will do the first examples as a class, then they will work individually to get the answer : 12 jumps.
Problem 2:   20 -__=15 We will model starting at 20. Asking How many jumps do we have to make backwards to get to 15? We will do this in red. The answer is 15.

Perhaps the design just needs a tweaking from the original concept. It is possible observing the children’s’ strategies to uncover their thinking which we can realize why it failed to work or possibilities of what needs to change. It would be important to ask the set group of students why it didn’t work for them and most importantly ponder on their answers.

In summation, if all these approaches failed, we would move on to a different tool to help further the classes’ understanding of addition and subtraction. Ultimately, we must create a tool that supports the learners’ conceptual understanding of how adding and subtracting works.

Works Cited

Van de Walle, John A. Teaching Student-Centered Mathematics. Developmentally Appropriate Instruction for Grades 3-5. Boston:Pearson, 2014

“Fraction Friend”

February 16, 2017

We decided to create a design that would help students better understand fractions and how they relate to whole numbers. As young learners, Kerri and I struggled with the concept of fractions. This included how to add and subtract fractions and conceptualize how many “pieces” would make up a whole. We were inspired by this challenge to create a tool that will allow students to visually understand different types of fractions and how they relate to one another.

Our idea stemmed from the idea of stacking blocks that while similar in size, represented different fractions. We decided to use a circle as we felt this shape would be the easiest for young learners to understand that different fractions, when combined, create new fractions and sometimes whole numbers. We wanted to create five circles that represented different fractions. Each circle will slide onto a base. We felt this would encourage interaction between students and act as a building game while also familiarizing the students with fractions. The first circle of the stack represents one whole circle. The second circle is divided into halves. The third circle is divided into fourths. The fourth circle is divided into sixths. The final circle is divided into eights.

We think this should work from a mathematical learning point of view because it is a great visual aid for students who have difficulty understanding fractions. Students are able to compare and contrast the circles to understand how fractions relate to one another. For instance, a student may observe that three slices of 1/6 are the same as one slice of a 1/2.

The design of our technology reflects our understanding of what mathematics is and of how learning happens as it focuses on the visual aspect of learning fractions. According to Empson and Levi (n.d.) the development of children’s understanding of fractional quantities begins in the processes of creating fractional parts by drawing, cutting, folding, and splitting things and then reflecting on the results (p 22). Young learners understand best when visual representations are accessible to problem solve. Our design helps students compare the size of fractional parts to a whole unit.

For our project to be successful in terms of learning, we would hope that students who use our design would be able to visually understand fractions more easily, work interactively with others, and enjoy building different representations of fractions and numbers. We hope our visual would aid in homework help when students are having difficulty understanding fractions on paper.

We’re hopeful our design will be a successful tool for students to readily use. However, in our initial brainstorm, we had hoped to create an object that would allow students to remove each piece of the circle to play with different combinations of fractions. If a student is unable to visualize multiple representations of fractions at once, this may confuse the student initially. However, our goal is for the student to be able to look at a fraction with multiple parts and understand what each piece means as it relates to the fraction or whole number. Our hope is that the visual aspect of our design will aid in the overall comprehension of fractions.

In regards to testing our design, we thought it would be appropriate to give our model to young members of our family. Jess will allow her nephew (age 8) and Kerri will allow her cousin (age 9) to test out the design. We use observe them interacting with the tool and use their feedback as a form of assessment for understanding. We will also test the design ourselves. Since we both struggled with fractions as young learners, we will use our prior knowledge to determine if the tool is successful in solving fraction related problems. If we are able to clearly understand how fractions relate using our tool, we have successfully completed our task.

“Fun with Fractions”

February 16, 2017

Because children utilize a myriad of different strategies to problem solve, the intention of my manipulative is for children to have an additional tool that they can use to help them work through equal share problems. My manipulative will serve as a visual representation of groups and how they can distribute whole, half, third, and quarter pieces to groups. Since some children have non-anticipatory coordination between groups and shares, my manipulative will be a way for children to utilize the pieces to see the distribution of shares to each group. They will be able to move pieces around to see the dynamics of how choosing different pieces will affect the groups and the shares. Additionally, equal sharing problems “allow children to create and manipulate fractional amounts and to reflect on the relationship between the numerator and denominator” (Empson, 2011, p. xxv) so children will be able to utilize my manipulative to begin gaining the concept of numerator and denominator which will demonstrate their understanding of parts, wholes and parts of wholes. Even without a specific word problem to work through, children will have the opportunity to tinker with the board and the pieces to find the relationships between the pieces and the groups.

I decided to make an 8×8 grid where children can use pieces to “fill in” or represent equal share problems. The grid is slightly raised and each square is hollow to allow for pieces to be inserted into each square. I decided that after the product (which is white) is printed, I will color in each “box” of four squares with a color. For example, the first “box” of four squares will be black, the second “box” of four squares will be pink, the third “box” of four squares will be black and so on so that children will have 16 groups (each delineated by being either black or pink). From there, children will have a variety of pieces from which to choose. One “whole” piece represents “one whole,” one half piece represents “one half of a whole,” one third piece represents “one third of a whole,” and lastly one quarter piece represents “one quarter of a whole.” Each of the pieces will be sized so that children can see the differences between the pieces to demonstrate larger and smaller units (ie: the one third piece will be bigger than the one quarter piece) and how they relate to one another. They will learn how parts combine to equal one whole.

Because children solve problems utilizing different strategies and models of representation, this manipulative will be one tool that students can decide to use while working through equal share problems. As the teacher, it will be my responsibility to properly launch the tasks and ask pointed questions where appropriate. However, I want students to work through their problems utilizing the modes and methods that are most helpful to them. Children will be encouraged to work together to discuss rationales for their work and to learn from one another. This manipulative will allow for great conversations as students work to discuss why they decided to use the tool, how they used it and what they learned from using it.

Since “equal sharing problems where the answer is greater than 1 are easier for young children” (Empson, 2011, p. 10), this manipulative will allow students to work through such problems. Problems will be designed to include a total number of items to evenly distribute. Additionally, “solving and discussing equal sharing problems prepares children to learn from a variety of other problems involving fractions and decimals” (Empson, 2011, p. xxi), therefore this tool will help to prepare children for future concepts. The manipulative (and other representations) will provide insight as to how the child interprets and thinks about equal sharing. The manipulative will also allow students the opportunity to visualize their thoughts and to make sense of their processes; the tool will be another way that students can communicate their ideas and provide rationale as to how they arrive at their solutions. Similarly, since equal sharing problems build off multiplication and division (partitive more specifically), I will present this manipulative after the concepts of multiplication and division have been introduced and taught.

The success of the manipulative will mean that children can make sense or are working toward understanding what it means to equally distribute shares. The success of the manipulative will mean that children have or are working toward understanding the difference between a whole, half, third, and quarter and how those shares when manipulated can equal one whole. The success of this manipulative will mean that children have the ability to utilize different mediums to work though problems and will be able to explain their thought processes based off their work on the manipulative.

If my design failed to work, I would garner information from children and teachers as to why they did not like working with the product. In efforts to improve the manipulative, I would want to know if the design, the aesthetics and/or the functionality were the reason why they preferred to utilize other methods over my manipulative, and I would ask for suggestions for improvement.

For testing, I can imagine presenting children and teachers with this manipulative coupled with some equal share problems. The reason why I want to test this product with teachers as well is because I believe teachers need to be comfortable utilizing the manipulative prior to presenting this tool as an option for students. I can imagine observing to determine what types of tools they use to problem solve as well as the strategies they use to solve said problems. I can imagine wanting to determine if my vision for the use of the manipulative is how children and teachers actually utilize it. I also want to determine if the users thought any part of the design was confusing, and if they had any suggestions on how to improve the manipulative. I want to know if they prefer utilizing the manipulative over other methods and the rationale for their decision. I want to determine if children and teachers solely utilize the manipulative, another method or a combination of both. I can imagine asking questions as to any ideas to better improve the product. Ideally, after the test and receiving feedback from the children and teachers, I would make any necessary changes and have the children and teachers utilize the new model for their feedback on the enhanced product.

Even Number Tool

February 16, 2017

For my 3-D design project, I designed a manipulative that I believe will help students learn what an even number is. As we discussed, it is better to learn what something is and understand it, instead of simply memorizing the facts. Therefore, for my manipulative to help learn what even numbers are, I scratched my puzzle idea. In the end, I created a container and different edged prisms.

The purpose of the manipulative is to separate the pieces of each prism, one at a time, into the two sides of the container. An even number is characterized as, “Any integer (not a fraction) that can be divided exactly by 2” (Definition of an even number). Therefore, if both sides of the container have an equal number of edges, that means that the number can be divided equally into 2 parts, which makes the number even. I think this manipulative should work from a mathematical learning point of view, because the two parts of the container represent the two halves of the whole. When the two halves have the same amount of edges in them, it will show that the number of edges can be divided by two equally.

The prisms, when looking at them from above, have four to seven edges. The amount of edges per prism represents both even and odd numbers. This will help students really have to think and not assume that a number is even based on if the number of edges is a number included in this manipulative. Since the students cannot assume, they will have to think and try to understand why having two edges on each side makes the prism’s number of edges a number even. Students will also have to try to understand why two edges of the prism on one side of the container and three edges of the prism on the other side will help prove that the number of edges to that particular prism is not an even number. This should help students learn what even numbers can be when working with the design I have created.

I feel that learning often happens through exploration and believe that children often learn and work better when they have manipulatives to use. Those beliefs, along with my understanding of math led to my design of the manipulative. I feel that there are enough prisms to explore with, for younger elementary school grades, and the container to go with it helps the students separate the pieces in a way that the pieces can be counted without necessarily putting them all back into a single pile. The design also allows for some flexibility. Students can count the number of pieces per container as they go along, or they can separate the pieces and then count each side after the edges have been placed into the two sides of the container.

In terms of learning, my project would be considered successful if students were able to use it as a manipulative or even as a math center. I hope the project could be used for students to explore and better learn what it means for a number to be considered an even number. The students would be able to explore and see what an even number is. This could even be used as in introduction to even numbers. For example, a teacher could give them to students and say which prisms have an even number of edges and which have an odd number of edges. From there, students would have to use their imagination, think critically, and fully involve themselves with the design to look for possibilities to why the even numbers are even and why the odd numbers are not even.

If the project was successful, it could even help teach the students how to tell if a number is odd. The students can learn that an odd number is not a number that equally divides by two. From the knowledge they learn, they can see the differences. Students could also come up with their own reasoning that the design allows them to think of for why an odd number is odd.

If my project failed to work, there would be at least one of two reasons behind the failure. The first reason of failure would be the reason for me not doing a puzzle. The project would fail if students memorized the rule for even numbers, instead of using the design to explore and learn. The second reason that the project would fail to work, would be if the students were unable to comprehend how to learn about even numbers from the design. Since this particular manipulative was designed, with the purpose of helping students learn what an even number is, the project would fail if students were not able to come to the conclusions or if students struggled using the manipulative in general.

In terms of testing my design, I have a few options. My first option would be to see if the teacher I work for would allow me to test the project in the classroom of 5. The class is an LLD classroom for Grade 1 and Grade 2 students. The age group and capabilities in math would be appropriate for the project, and the students would help me see the project being tested out in a real-life, classroom setting.

My second option would be to reach out to my mother’s friends who teaches children in K-2 and have those children test out the design. I could see a few children at two different times based on locations in New Jersey (some live in North Jersey and some live in South Jersey). I could have one group use them knowing beforehand what makes an even number even and have the other group use the project not knowing what makes an even number even. This would show me if the project could be used both ways in a classroom.

If neither of the two are doable options, I can reach out to my father and step-mother. I have a half-sister who is in Grade 1, so she would also be an acceptable grade level to test out my project on. With my three options and option 2 having some flexibility, I know that I can test out the project without any issues.

Addition and Subtraction Tool

February 16, 2017

Our manipulative would be best used by a young child in preschool or kindergarten, who is learning addition and subtraction. The user would learn addition by putting a certain number of small cubes in one side of the pipe design on the top of our manipulative, and another amount of cubes in the other side of the pipe design. The cubes would funnel down to the bottom of the manipulative, a box with a tray, and the child could find the sum by counting all of the cubes. For example, if the child puts three cubes in the left side of the pipe, and two cubes in the right side of the pipe, they will find five cubes in the tray at the bottom of our manipulative. The child will see that three plus two equals five.

If the child flips our manipulative upside down, they can learn subtraction. The child can put a large number of cubes in the box part of our manipulative, and the cubes would funnel out of either side of the pipe design. There will be another tray on the bottom of our design, which will catch the cubes, but keep them separated, so the child knows which pipe they came out of. For example, if the child puts five cubes in the box part of our manipulative, and three cubes come out of one side of the pipe, and two cubes come out of the other side of the pipe, the child will see that five minus three equals two.

According to Walle, Lovin, Karp & Bay-Williams (2014), “Any time a concept is new, regardless of the ages of the students, manipulatives can help make the concept visual, concrete, and connected to other ideas students have learned” (pg. 24). Our manipulative will give young students a visual idea of what happens when you add or
subtract. Our manipulative will be even more effective, if the teacher provides meaning
to what the cubes mean. For example, instead of saying “there are three cubes”, the
teacher can say, “Imagine that these cubes are apples. Billy picks three apples from one side of the tree (puts 3 cubes in the left side of the pipe) and picks two apples from the other side of the tree (puts 2 cubes in the right side of the pipe). How many apples did Billy pick from the tree (lifts box to reveal 5 cubes in the tray)’. According to Walle et al. (2014), “Manipulatives alone have no inherent meaning. A person has to impose meaning on them. The manipulative is not the concept” (pg. 24).

In terms of learning, our addition/subtraction manipulative will be considered successful if the student understands that the combination (or separation) of balls yields a certain amount. Not only do we want the child to know simple addition and subtraction problems from memorization, but we want them to be able to understand that by physically combining two sets of objects, or separating them, you will either get more or less of those objects. The way our manipulative is set up, it allows for the answer to be hidden. For example, if a student were to put two balls in one side and two balls in the
other, they can guess the sum without seeing it. This will help provide us insight into how much the student understands about addition and subtraction.

As the child continues to use the manipulative, it is our goal for them to eventually be able to predict the outcome. If a student has never been exposed to any type of addition/subtraction problems before, it may take a few attempts to grasp the concept. However, after using the manipulative, the child should understand If after using the manipulative for more than one or two math lessons the child is not able to predict the outcome, for addition problems, we will know that it was unsuccessful. For example, let’s say a child is given multiple simple addition problems such as 1+2 =?, 4 +4 = ?, and 5+2 =?. After putting the objects into the manipulative they should get 3, 8, and 7, as end results. The child should eventually understand that prior to putting the objects down each tube, if they counted all of them together, they would get the same sum as they would when the objects go into the box. If the child does not grasp this concept, our manipulative has failed.

Our manipulative can work with both simple addition and subtraction problems, and simple addition word problems. To test our manipulative, simple joining word problems may work best. For a joining, or addition problem, we will have a starting quantity, a second (change) quantity, and the final result (Carpenter et al., 2015). An example of a problem would be, “Amber had 4 muffins. Her mom gave her 5 more muffins for snack. How many muffins did she then have?” The child will begin with 4 objects down one tube and add 5 objects down another tube, and she will get 9 objects altogether. In hopes that the child understands what the manipulative is representing, she will answer “9 muffins”.

When it comes to subtraction, word problems will not work. This is because the way our manipulative is set up, both the change and result will be unknown. Therefore, a word problem cannot be presented. The subtraction aspect of our manipulative does not allow for a child to “guess” the result. When the manipulative is turned upside down, a child begins with a larger quantity, say 10, and the objects will divide between the two tubes (we cannot predict how the objects will divide). When the manipulative is picked up, the child should know to begin with the first number (10), and look at the objects in the tray that came out of the left tube, let’s say 4. She will then say “10-4=..”, and look at the number of objects that came out of the right tube, which will be 6. Her end result will
be “10-4=6”. Understanding that a number can be separated into two different, smaller parts is the main idea.

Overall, the idea of our manipulative is to make sure our students have a full
grasp of what subtraction and addition means. Memorizing addition and subtraction facts
may be useful as they get older, but understanding why these problems make sense is
what will further help them in school.

References
Carpenter, T., Fennema, E., Franke, M., Levi, L., & Empson, S. (2015). Children’s

Mathematics: Cognitively Guided Instruction. Portsmouth, NH: Heinemann.

Van de Walle, J. A., Lovin, L. H., Karp, K. S., & Bay-Williams, J. M. (2014). Teaching
student-centered mathematics (Vol. 2, Grades 3-5

Area, Perimeter and Ratio Tool

February 16, 2017

We are proposing a tool that will help students determine area and perimeter. Our tool will consist of rectangular 2D frames. The dimensions of the whole figure (side lengths) will be a ratio of the inner frames dimensions (1:2, 1:3, etc.). Our goal is to have students realize the relationships between perimeter and area when the dimensions are changed. What happens to the area and perimeter of a figure when a figure’s sides are cut in half (or doubled)? In thirds (or tripled)? Students will also be able to practice calculating area and perimeter.

Students will be able to physically hold the figure and count the lengths of the sides, allowing the mind and body to be fully engaged while calculating perimeter and area. Students will be able to take multiple frames in order to draw more meaningful connections about perimeter and area, and the relationships created between figures and their ratios.

We believe our tool will allow students to have a great hands-on experience. They will not only be able to visualize, but will be able to physically manipulate the tool while forming thoughts and connections about area and perimeter. The physical nature of the tool and the manipulation that will occur will help a child’s fine motor skills. Instead of just listening to steps and memorizing sequences, the children will ideally be able to understand in a deeper context the relationship between altering a figure’s dimensions and what that means for the perimeter and area.

If our tool is successful, the students using it would attain knowledge about side lengths, perimeter and area. If our project was successful, it would mean the relationships between side length, area and perimeter would be clearly found, recognized and understood by students. For example, students would see that cutting the sides of the original frame into thirds would create an equal ratio for the perimeter (1:3), but the area would be a 1:9 ratio.

If our tool were to fail to work, this would mean that we may have a misconception about the relationship between dimensions of a figure and area and perimeter. If our tool failed, it would mean that it was not designed properly to show an accurate relationship between area, perimeter and side lengths.

To test out our design, we could give students pictures of shapes and ask them to find the perimeter and area. These formulas could be provided, depending on level of students. We could then ask the students to determine relationships between the original figure, and figures that have a half or a third of its side lengths. If they can figure out the relationships and ratios, we could then discuss why these relationships occur.

Learning Fractions Tool

February 16, 2017

When it comes to learning fractions, some children might take longer to grasp the concept of an amount being less or partially more than a whole number. For this reason, teaching students about fractions might require various different strategies that can reach struggling students. A physical representation of fractions would really help problems come to life in a much…

Place Value Tool

February 16, 2017

When first thinking about making a manipulative for this making for learning project, we both thought about what would be the most beneficial tool for the grades we were teaching. We had conversations about what we thought our students were struggling with the most, and we both came to the conclusion that our students needed to work on understanding…

3-D Fraction Blocks

February 16, 2017

How is the user of your manipulative supposed to learn from working with your design?

Studies have shown that “students who use concrete materials develop more precise and more comprehensive mental representations, often show more motivation and on-task behavior, understand mathematical ideas, and better apply these ideas to life situations,” (Hauser).

By using this manipulative that I have designed, I am hoping that the user will gain a better understanding of fractions. Fractions are often taught using 2-dimensional figures, graphics or manipulatives. Using 3 dimensions, students can better understand fractions through increased spatial awareness while introducing area and volume concepts at an earlier age if desired, as well. Using the blocks will give the student the chance to explore how a whole can be divided into equal parts. Additionally, the blocks can also be used to explore equivalent fractions or missing parts of the whole.

How does the design of your technology reflect your understanding of what mathematics is and of how learning happens?

In order to succeed in mathematics, I believe that students must develop an understanding of abstract concepts first. Additionally, learning the concepts of fractions specifically can be one of the most difficult skills to master for elementary level students. With so many different ways to expose students to manipulatives and enhance their fraction learning experience, it is important to examine how effective these teaching tools can be first.

These concrete materials are meant to assist children at all levels of education including understanding processes, communicating their mathematical thinking, and extending their ideas to higher order thinking levels (Balka, 1993). In addition, using manipulatives enables students to make connections with other mathematical topics, gain insight to other academic subject areas, and in their personal interests and experiences (Lee & Chen, 2010).

Therefore, just like I believe that fractions can be simple to understand, this manipulative is intended to be simple to understand. Also, just like math is meant to make our lives easier, so are the use of these manipulatives. Sometimes all it takes is to see something from a different perspective for it to make sense. Every child learns differently and children understand differently, so by giving the child a chance to make sense of something on their own terms, makes a huge difference.

What would it mean for your project to be successful in terms of learning?

If I were able to get a student to verbalize mathematical thinking while discussing mathematical ideas and concepts, and gain confidence in their ability to find solutions to mathematical problems using methods that they came up with themselves without relying on direction from myself or the teacher, then I would consider it to be successful in terms of learning.

With this project, my intention is to give the child a way to learn about fractions, while making the learning process more fun and engaging. I am also attempting to demonstrate a significant amount of student growth when being assessed. Furthermore, after using my design, I would like the students to be more willing to share ideas and explore concepts when it comes to fractions, as well as ask and answer higher order thinking questions.

Finally, in order for this manipulative to be considered successful in terms of learning, I would like the use of it to allow students to communicate their thoughts and ideas about fractions and what they have learned to other classmates, who may still be struggling, more easily.

What would it mean if it were to fail to work?

If this manipulative fails to work, it would mean that it was not an efficient enough tool for use. The goal is to help children understand the idea of fractions while building a strong understanding of mathematical concepts. If this manipulative cannot efficiently do that, then it has failed. Additionally, the idea of a manipulative is to correctly portray the actual math lesson or concept intended, while instilling a sense of understanding to the given topics. This means that if the manipulative is not effective, then it will not help the student understand the mathematical concept, and instead it may even confuse them further. Not to mention, we would like students to be able to use the manipulative in order to further their understanding so that they are able to explain it more clearly to other students who are still struggling, not lead them astray.

Finally, if after using this design, students still can’t enhance their achievements in mathematics, specifically when it comes to lessons regarding fractions, then it has failed to work.

What kind of testing could you imagine carrying out for your design?

I would use my design for a number of different tests. First, I would test out this manipulative with teachers. I would see what they think of it, and ask for any feedback on what is it about the product they initially like and don’t like. I would then ask if they would try it out either in their classroom, or with students they may tutor independently or after-school. Then I would collect more feedback from them based on how it helped their students or didn’t, and if they would consider continuing to use them. This information would also be further used in case studies I would complete regarding the effectiveness of this design.

Then I would like to test it on children, out of school first, preferably with a variety of different age and grade levels. I would like to see what the children’s initial thoughts about the product are, un-relative to math. (What they think it is, do they like the colors, aesthetics of it, what they think it is used for?) After that, I would introduce it to those children as a manipulative used to understand mathematical concepts, and explain how it can be used. I would also use this information for my case studies that I would be completing regarding this specific design.

Finally, depending on the information I gather from the first two test subjects, I would like to carry out some tests using this product with parents. Often these are the people who work with their children the most, and it is important to see if this is something that they find useful or not. It would be interesting to get the thoughts and opinions about the manipulative, from adults who potentially have little understanding themselves, of the concepts of mathematical ideas. Was it something they were able to easily understand? Was it something that they were easily able to explain to their children when helping with things like homework and studying? Again, this would be included in my case study that I would be doing for this design.

REFERENCES

Balka, D. S. (1993). Making the connections in mathematics via manipulatives. Contemporary Education, 65, 19-23.

Hauser , Jane. Concrete-representational-abstract instructional approach. Retrieved April 9, 2009, from the Access Center: Improving Outcomes for all Students K-8. Web site: http://www.k8accesscenter.org/training_resources/CRA_Instructional_Approach.asp

Lee, C., & Chen, M. (2010). Taiwanese junior high school students’ mathematics attitudes and Perceptions towards virtual manipulatives. British Journal of Educational Technology, 41(2), E17-E21. doi:10.1111/j.1467-8535.2008.00877.x

“The Sphere”

February 16, 2017

In order to know the prior knowledge the student has about three dimensional objects a mini lesson on two dimensional versus three dimensional would be beneficial. In order to see their understanding of object in three dimension or two dimension I would place two bins labeled ‘3d’ and ‘2d’ and give the student a pile of objects to sort. …

Negative and Positive Number Line

February 16, 2017

Learning about positive and negative numbers is a concept that can fall prey to memorization of rules without understanding rationale. Negative values can easily become abstract and conceptual; unrelated to a concrete idea. Until the moment of learning negative numbers, students learn that all numbers represent solid quantities. Even when understanding fractions and decimals, the quantities can be represented…

Snub Cube

February 16, 2017

Math has never been my strong suit. I have always struggled with math and the idea of math. Before taking this class I have had a very low opinion of math. I can say that my feelings about math are still not the greatest, but they have improved slightly. I still cannot connect math enough to the real world…

Rates of Change Tool

February 16, 2017

Originally I wanted to do something that dealt with probability because I like gambling and that would have fun to make a math game out of. I soon learned that a lot of probability math games have already been invented and I would just be recycling an old idea and that not really my style. Next I was thinking…

Tactile Interactions with Numbers

February 16, 2017

I currently work in a classroom where six students fall somewhere on the Autism Spectrum Disorder. Working one-on-one with these students is often difficult because they have below average memory retention, making concepts harder to grasp and build upon. My students range in age from 2nd grade to 5th grade but all of them do work with numbers. Exercises include addition and subtraction, skip counting, and for some, simply writing out numbers. As instruction expanded into other areas such as reading, writing, music, etc. I’ve found the knowledge of numbers to be extremely important and widespread. Our students also tend to struggle with hand/motor coordination which ultimately affects their ability to independently write certain numbers and shapes. This difficulty is most often associated with the younger students. With all of this information, I’ve decided to create a counting tool to help my students work with numbers in a way that allows them to rely on a physical object. The fact that our work is created using a 3-D printer is wonderful because my students also greatly benefit from tactile touch within their learning experiences. My tool will be palm-sized written numbers 1-10 with a hole in each number indicating its value or ‘how many’. For example, there will be one hole in 1 and ten holes in 10. I’m hoping this will allow my students to not only visibly see the written representation of numbers 1-10 but to also physically feel what each of these individual numbers represent.

Throughout the chapters that we have read in both of our textbooks, direct modeling forms the basis of how students begin to develop their concepts of numbers and their corresponding values. The importance of representation as seen in direct modeling is something that I hope to embody with my counting tool. Students within the direct modeling stage are not able to abstractly work with numbers presented to them so their reliance on physical representation is key. I want my tool to align with the goal similar to that of Children’s Mathematics: “to provide a basis for developing understanding of basic number concept and operations by connecting them to children’s surprisingly rich intuitive conceptions and giving them an opportunity to extend these concepts in ways that make sense to them” (Carpenter, Fennema, Loef Franke, Levi, Empson, 2015, p.5). My decision to add holes to each of the numbers is with the hope of encouraging my students to make their own personal conclusion as to what each hole represents. Some may need to look and touch all ten numbers in order to understand, others may only need look. I want my students to reach this conclusion on their own so they come to terms with the written and valued representations of numbers 1-10 supported by their own thoughts, ideas, and connections.

This tool values the importance of the role that tangible interaction and hands-on-experience plays within mathematics. In order to continue and build upon number problems and operations, students need to feel comfortable understanding what a number means. Being able to have a visual representation of a value is a crucial foundation in furthering math capabilities and overall confidence. Numbers 1-10 also allow students to observe the patterns that are formed within the base ten system. Additionally, counting strategies can be made more accessible when students are able to tangibly recognize and ‘feel’ number relationships. A hundreds chart has been known to be helpful for students to recognize certain patterns amongst number groups but this tool doesn’t provide a hands on approach. We know that number facts are not learned by habitual repetition. My tool can be the bridge that gaps the hundreds chart to a more abstract concept of number facts. The pieces are interactive and can be used in a variety of different situations.

In order to measure the success of my tool, I would hope that my students would be able to make the connection of written and valued representation without the help of physical objects. I do think it’s important though, that my students take their time in order to get comfortable with the tool and use it for a variety of number related concepts, not just simple counting from 1-10. If I were to say a number aloud and then my student could show me (with fingers, counters, tallies, etc.) how much that number represented then I would consider my tool a success. If the tool failed, my students would not have been able to make the connection between the written and valued representations of the provided numbers. This would not be their fault but a fault in design that I would need to work to adjust after observing the challenges it presented to my students. I wouldn’t want my tool to be used in any type of testing, I only want it as a support system for my students. If it doesn’t work, it is my responsibility to fix it. If it does, then that’s wonderful for the students who it helps. The testing aspect gets too technical and takes away from the purpose of the tool which is just to give some students a different way of learning or understanding new or difficult information.

Fractions Tool

February 15, 2017

When designing this project, I was not sure what I would be designing or how I would be achieving it. I did know one thing; I wanted it to be about fractions. As a child, I had so much trouble with fractions. Looking back now, I think the issue was that I didn’t understand that a fraction is a…

This material is based upon work supported by the National Science Foundation under Grant No. 1812887. Copyright © 2024.