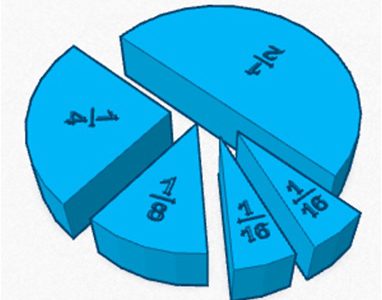
The learning tool I have created is a modified form of a fraction circle. Typically, fraction circles are designed with entirely equal parts; that is, a fraction circle will represent (for example) thirds or quarters and be broken into three or four equal parts respectively. While this has educational value in its own right, the modified form I have devised is composed of varying fraction sizes within the circle. Specifically, this fraction circle is a representation of the division of duples. The largest piece represents a half, but rather than the other piece also being a half, it is broken into quarters. One of these quarters is broken into eighths, and one of the eighths is broken into sixteenths. Though this tool is restricted to only demonstrating a division of two, it has its own purpose that standard fraction circles are not able to achieve. Not only does it allow the learner to be able to visually compare the different sized fractions composing the whole circle, but it allows for them to also understand the relative proportionality of each piece (two eighths make a quarter, two quarters make a half, etc.). This allows for this one tool to be used in various contexts and for various fractional proportions—likely with greater application than a standard fraction circle. Additionally, since divisions by half are so common in the world around us, there are many potential cross-curricular tie-ins (such as to music and the division of rhythmic beat units in duple meters), and real-world applications (such as to measurement and the division of inches in the Standard system).
With this tool, the learner is not limited to visualizing how all the parts collectively make a whole (as is the case with typical fraction circles). In one possible application, the student can use smaller parts and put them together to create other fractions of the circle. For instance, they can take the two one sixteenth pieces and put them together to not only form one eighth, but also relate them to the existing one eighth piece in order to visualize the comparative size. Providing learners visuals while teaching fractions is essential in helping them understand these concepts. For example, as Van de Walle et al. (2014) points out, “students may be told the bigger the denominator, the smaller the fraction. Teaching such rules…may lead them to overgeneralize that 1/5 is greater than 7/10.” In this way, students are missing essential learning opportunities when they are not provided with visuals and are limited to verbal explanations of rules. This modification of the fraction circle allows for yet another visual and kinetic tool to be used in the classroom encouraging learning, and for expansion to second and third level proportional associations.
Students must be provided with concrete tools to help them grasp these concepts. Van de Wall et al. (2014) also finds that, “students often do not explore fractions with a variety of models or do not have sufficient time to connect the models to related concepts. In fact, what appears to be critical in learning is that the use of physical tools leads to the use of mental models, and this builds students’ understanding of fractions.” This tool supports students in their exploration in understanding mathematical concepts and relationships. The teacher plays a critical role in mediating the use of mathematical learning tools which can enhance students’ learning. As was mentioned previously, once students are able to visualize the relative proportionality of various divisions of two through use of this manipulative, they will then be more likely to be able to successfully solve problems that include fractions, and, to Van de Wall’s point, will be able to apply this knowledge to other disciplines and applications in which these proportions appear.
To this end, successful application of this manipulative would be twofold. Firstly, learners will have an understanding of fractions and the concept of how fractions operate. At the base level, the student would be able to use trial and error to compare equal parts. Additionally, learners are able to build upon prior knowledge of whole numbers to be able to show how fractions are alike and different within whole numbers. As was noted earlier, since the tool will provide two of the same sized part (one sixteenth), they will be able to see that these two parts combined are equal in size to one eighth. These two eighths are then equal to a quarter. Next, these two quarters create a half, mirroring the piece of the manipulative representing one half. Ultimately, we want students to be able to grasp how fractions, when combined, create a whole. We want them to understand how the whole is composed by which pieces, or fractions, that they come to discover on their own and eventually are able to create a mental image of. Additionally, they should gain the perception that fractional pieces themselves are made up of other, smaller fractions—a property this tool demonstrates that existing fraction circles often do not.
Second, and perhaps more importantly, students will be able to use this knowledge in real-world applications. A logical extension activity (once the basic understanding of division and multiplication of fractions by two is understood) would be to the Standard ruler. This manipulative (alone or in multiples if measurements larger than one are involved) could be used to demonstrate and calculate addition and subtraction of fractions of an inch. Often young learners can struggle with this concept at first, and the use of a manipulative designed in this way could prove quite successful towards providing a concrete, visual means of assisting in these types of calculations of measurement that are necessary in virtually every walk of life.
Failure of the design to work would be evident in the original application of the tool. While it would be tempting to use successful completion of an extension activity (such as adding and subtracting measurements) to evaluate the success of this design, too many variables are at play for this to be a conclusive assessment on its own. Rather, the use of the tool itself is the best judge. Students should be able to use this tool to understand the relative proportions of halves, halves of halves, etc. Any duple divisions (up to sixteenths) and how they relate to their counterparts in the fraction circle should be fair for assessment after implementation of this tool. If the majority of students are unable to understand this concept, then the tool would have failed.
As such, testing of the tool should begin by probing students’ understanding of this concept. Through various questions (perhaps related to circular foods, such as pie), starting at the very base level (“what piece represents a quarter of the pie?” and “what piece represents half of that?”), ultimately we would want students to be able to answer questions constructed in the following form:
“If you have half of a pie, and you split your piece in half to give one piece to a friend, what fraction of the whole pie do you still have?”
This tests multi-layered understanding of fractions and their proportions to one another and examines the ability to make second and third tier determinations as to fractions—the essential goal of the tool. Use of the manipulative should culminate in a thorough understanding of this concept, and a successful test is one in which this knowledge is demonstrated.
Once this has been determined to have been achieved, application and implementation of this knowledge via the previously mentioned extension activity involving use of the manipulative as a visual aide in computation of problems concerning the addition and subtraction of measurement could adequately test the secondary goals of its function. Problems could begin by asking what one eighth of an inch plus one eighth of an inch is equal to, and progress to more complex problems that include whole numbers (such as 1 and 1 quarter inches plus 2 and 1 eighth inches). If students are ultimately successful solving these types of equations, then the manipulative would have been proven to work not only at its basest level, but also in its secondary function as a visual aide in application.